OBJECTIVO:
- Explicar de forma clara e com a maior simplicidade possível, a análise de resultados dos exercícios aqui propostos.
São postados vários exercícios e respectiva resolução, mas, o mais importante é a explicação da sua resolução.
Propomos a resolução de alguns exercícios, dos quais, apenas são ilustradas as soluções para que possa verificar seus conhecimentos.
Na eventualidade de surgirem dúvidas, o que é normal, poderá com certeza expô-las. Trataremos de analisá-las garantindo que o seu problema seja resolvido.
"A FORMA COMO SE OLHA PARA A MATEMATICA É O SEGREDO".
DERIVADAS
Definição de derivadas:
Derivadas: por definição as derivadas representam a taxa de variação de uma função....
Derivadas (individual, obtida empiricamente): como o próprio nome indica "derivada" traduz de onde provêm uma função qualquer ou de onde ela deriva/ou, o que lhe deu origem, etc...
Assim a adaptação deste segundo conceito pode levar a escolha certa do cálculo em causa, dependendo, da interpretação que lhe é atribuída.
Regras de derivação:

Derivadas essenciais:
Regra nº 1: (k' = 0) - Derivada de uma constante:
Segundo a regra assume-se k como sendo uma constante, simplificando; uma constante é um número qualquer (pertencente a qualquer dos conjuntos de números).
Exemplo:
Regra nº 2: (x' = 1) - Derivada de x:
Assume-se x como a variável de uma função; em uma função a variável poderá ser definida por outra letra qualquer normalmente é usada a letra x.
Exemplo:
Regra nº 3: (k . x' = k) - Derivada de uma constante multiplicada por x:
A derivada da multiplicação entre uma constante e a variável x é igual a própria constante como se pode verificar no exemplo abaixo onde é utilizada a regra nº 7 (derivada da multiplicação).
Exemplo:
Nota: Atenção aos casos em que x apresenta um grau maior que 1 quando assim for a regra a utilizar será a regra nº 4.
Regra nº 9: (k' = 0) - Derivada da potência de base x:
Alpha é igual ao grau da função derivada, repare que o grau da potência decrescente sempre em -1 relativamente a potência inicial.

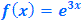




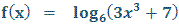









Comentários
Postar um comentário