Padrão de Turing, Sequência de Fibonacci e Girassóis.

Escrito por: Fernando Francisco em Destaques.

Biomatemática é a aplicação de métodos matemáticos em estudos da biologia como crescimento populacional,  desenvolvimento de manchas, tumores e citogenética, nesse artigo falaremos das contribuições de Alan Turing na biomatemática, sequência de fibonacci e padrões matemáticos na biologia.

O matemático britânico Alan Turing, não só se destacou pelas notáveis contribuições para a Ciência da Computação. O herói de guerra, responsável pela quebra de códigos nazistas durante a Segunda Guerra Mundial, idealizador e criador da chamada Máquina de Turing que deu o  alicerce para o que hoje é vangloriado como “algoritmos”, além de um assíduo observador da natureza é digno de uma verdadeira miríade de  ricos reconhecimentos em sua heráldica carreira científica.  Sua elucubração não se limitou apenas à criptografia  e à computação: Foi um notável estudioso da natureza.

A Sequência de Fibonacci.

A sequência de Fibonacci pode ser evidenciada, visualmente ou não, em diversos sistemas naturais. Em conchas, na face humana e no crescimento de flores, a sequência matemática, dada por n elementos pertencentes ao conjunto dos números naturais  definida por:

…

Onde um algarismo é a soma de  dois números antecedentes, está presente em diversos pontos da observação natural.

Note que: 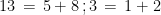 e assim por diante.

Temos por interpretação geométrica:

O número ao centro do quadrado é o valor de sua aresta. Perceba que a tendência dessa representação é crescente, formando um espiral. A soma da aresta de 8 com a de 13 resulta em um quadrado de lado 21. Repetindo  o processo, temos: , que é a aresta do novo quadrado “complementar”.

O que torna essa sequência ainda mais extraordinária é o chamado “número de ouro”. Faça um teste: selecione um número qualquer da sequência, como por exemplo o 34. Agora selecione o número anterior a ele – nesse caso o 21. Faça a divisão entre eles – deixarei o leitor usar a calculadora. Se as regras convencionais da divisão não estiverem, por inconstante, equivocadas, temos que:

A afirmação é a seguinte: toda a divisão de um número pertencente à sequência de fibonacci por seu anterior se aproxima de 1,618033. Chamamos esse algarismo de Número de ouro (simbolizado pela letra “phi”). Ele é irracional. Quanto maior for o número selecionado – e por consequência o seu antecessor – mais próximo o valor da razão se aproximará do número de ouro.

A contribuição de Alan Turing para a biomatemática.

Mas o que é biomatemática? De forma sintética, mas não delgada de informação, a biomatemática é uma aplicação direta dos métodos matemáticos e computacionais em estudos dinâmicos da biologia, sejam eles relacionados com crescimento populacional,  com o desenvolvimento de manchas e tumores e até mesmo com a citogenética.

A elucubração de Turing tem início na seguinte premissa: Dado uma relação com dois ou mais agentes,  é possível prever caracterísicas periódcas que resultam em difusões sistemáticas no dado evento estudado. Estes agentes manifestam ações recíprocas que podem ser previstas por modelos matemáticos bem definidos. Formam-se assim as Reações e difusões de agentes que caracterizam o Padrão de Turing.

Um exemplo elucidativo foi dado por James D. Murray em um artigo publicado em 1988 na revista American Science: Imagine uma floresta seca que está sendo consumida pelas chamas de um incêndio. Rapidamente diversos bombeiros se instalam na região  de maneira em que vários focos do incêndio ficam em evidência pelas mangueiras d’água. A forma como o fogo se espalha e a heráldica investida do corpo de bombeiros ao impedi-lá moldam diversas manchas cinzentas na floresta que podem ser observadas por sobrevoo. A mancha formada pela incêndio pode ser estudada pelo Padrão de Turing: Existem dois agentes nessa situação: os bombeiros e o fogo. A relação estabelecida entre eles, além de antagônicas, são recíprocas e formam as Reações. A forma como o fogo se espalha e, por consequência, as manchas estancadas são vítimas da Difusão sistemática causada pela interação dos dois agentes. Essa relação estabelece regras que podem ser estudadas por modelagem matemática.

Apesar das diversas aplicações – como o estudo  da mancha de animais como a girafa e a onça-pintada – a ideia foi apresentada por Alan Turing em 1951 por meio do estudo da Morfogênese. Foram elucidados em seu artigo os padrões e semelhanças dos processos embrionários de diversos seres vivos.

 A mais conhecida das investigações de Turing é a do “miolo do girassol”. Foi observado que a forma como os espirais de sementes do girassol se espalhavam no miolo era semelhante com o espiral de Fibonacci. Logo, seria possível identificar a proporção áurea ( número de ouro) na forma como os espirais se difundiam. Infelizmente Alan Turing, vítima da ignorância retrógrada da Inglaterra no século XX,  morreu antes de qualquer afirmação conclusiva.

A matemática no crescimento populacional.

Como são as diversas coisas na matemática, a representação numérica de um crescimento populacional em uma dada espécie é dada por uma função.  Pode então ser  de diversos tipos – no caso do crescimento bacteriano é uma função exponencial. A partir dela, estudamos uma coisa chamada “derivada” que expressa a taxa de variação, isto é , a forma como o valor da função varia ao longo de uma dada variável.

Considere então N(t) a função que expressa o crescimento populacional em um dado tempo ( em horas). A taxa de variação  (derivada) é dada por:

 

Esta coisa feia que está ao lado esquerdo da equação é a chamada “derivada da função N(t) em relação ao tempo t”. Caso o leitor ainda não tenha aprendido cálculo, não se sinta obrigado a entender como a derivada foi feita. Concentre-se em seu sentido. Perceba a intrínseca relação entre o número de indivíduos que nascem e a sua subtração pelas mortes e pela migração. Esta é compreendida da seguinte maneira: caso novos indivíduos entrem na população seu valor é negativo. Ao contrário – indivíduos que saem do nicho estudado – tem o valor positivo. Parece distante da lógica convencional, mas pela equação dada faz sentido.

Note que se o valor da relação entre Nascimento, morte e migração for negativo, a taxa de variação também é. Isso significa que a população está diminuindo. Em outras palavras, o número de indivíduos que nascem é menor  do que o número dos que saem da região ou vão, parafraseando o amado e odiado Machado de Assis, estudar a geologia dos campos santos.

E os girassóis?

Como já é tristemente conhecido, Alan Turing não pôde sintetizar seus estudos sobre os girassóis. Mas no Centenário do nosso herói uma instituição sem fins lucrativos foi fundada para tentar concretizar a tão genial observação do matemático. A Turing’s Sunflowers está reunindo diversas pessoas ao redor do mundo para registrar suas observações em girassóis. A parte mais elucidativa e fantástica do projeto é que você, caro leitor,  pode participar enviando as suas observações, e em síntese auxiliar diversos biólogos e matemáticos que trabalham com afinco nessa pesquisa.

Referências bibliográficas sobre biomatemática

1. Rodrigues, L. A. D., Seidel, D. J. e Mistro, D. C.: Padrões de Turing em um Sistema Presa-Predador. BIOMATEMÁTICA, 17: 65-72, 2007.
2. GUSTAVO, Luis Cristino , Alan Turing, o biólogo, UNESP .www2.unesp.br/revista/?p=5517
3. J.D. Murray Mathematical Biology: I. An Introduction
4. www.Educ.fc.pt/icm/icm99/icm17/curiosidouro.htm
5. www.educ.fac.ul,pt./icm/icm2002/icm203/números.htm

Fonte: http://cienciasetecnologia.com/biomatematica-allan-turing-sequencia-fibonacci/